[算法]关于vector的push_back扩容过程的经典问题

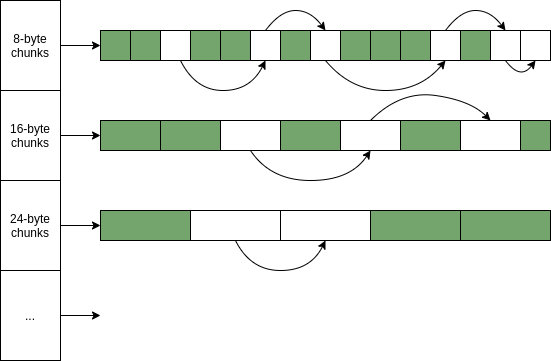
在面试c++开发过程中，我经常问STL vector的内容，这里面挖掘的内容比较丰富，不限于：

• vector的内存配置器实现（经典内存池）
• vector扩容策略
• at和[]操作符的区别
• 迭代器失效问题
• 打码实现一个vector

内存配置器

在STL标准下，内存配置器（allocator）是有标准的

// 申请内存空间
pointer allocator::allocate(size_type n, const void* = 0)
// 释放内存空间
void allocator::deallocate(pointer p, size_type n)
// 调用对象构造函数，等同于 new((void*)p) T(x) 
// new((void*)p) T(x) 为placement new，即在指定内存空间下构造函数
void allocator::construct(pointer p, const T& x)
// 调用对象析构函数，等同于 p->~T()
void allocator::destroy(pointer p)

SGI实现的allocator至少有两级，

• 第二级配置器使用自由链表实现内存池，可以有效减小频繁的申请和释放以及内存碎片问题。
• 第一级配置器直接简单封装的malloc和free。

扩容策略和均摊分析

接下来考虑常见的插值场景（第二个问题），当vector扩容时，内存申请策略为什么一般是扩展1.5或者2倍？

vector<int> = v; // start with an empty vector
v.push_back(1); // v = [1] and capacity = 1
v.push_back(2); // v = [1,2] and capacity = 2
v.push_back(3); // v = [1,2,3] and capacity = 4
v.push_back(4); // v = [1,2,3,4] and capacity = 4
v.push_back(5); // v = [1,2,3,4,5] and capacity = 8
v.push_back(6); // v = [1,2,3,4,5,6] and capacity = 8
v.push_back(7); // v = [1,2,3,4,5,6,7] and capacity = 8
v.push_back(8); // v = [1,2,3,4,5,6,7,8] and capacity = 8
v.push_back(9); // v = [1,2,3,4,5,6,7,8,9] and capacity = 16

template<class T>
void vector<T>::push_back(const T& val) {
    if (capac == 0) 
        reserve(1);
    else if (sz==capac) 
        reserve(2*capac); // 2倍扩容
    alloc.construct(&elem[sz], val); 
    ++sz;
}

template<class T>
void vector<T>::reserve(int newalloc) {
    if(newalloc <= capac) 
        return;
    T* p = alloc.allocate(newalloc);
    for(int i=0; i<sz; ++i)
        alloc.construct(&p[i],elem[i]); // copy
    // deallocation omitted ...
    elem = p;
    capac = newalloc;
}

我们可以统计元素的插入和复制的操作，计算一下每次插入的代价：

operation	capacity	cost(copy+insert)
push_back(1)	1	1
push_back(2)	2	1 + 1
push_back(3)	4	2 + 1
push_back(4)	4	1
push_back(5)	8	4 + 1
push_back(6)	8	1
push_back(7)	8	1
push_back(8)	8	1
push_back(9)	16	8 + 1

归纳一下，代价函数和总代价为：

\[C_i = \begin{cases} 1+2k &(if\ {(i−1)=2k}) \\ 1 &(otherwise) \\ \end {cases}\] \[T(n) = \sum_{i=1}^n{C_i} \le n+ \sum_{i=1}^{|\lg n|}{2^i} = n + 2n -1 = 3n - 1\]

均摊一下，平均代价为

\[c = \frac {T(n)}{n} = (3n − 1)/n < 3.\]

因此，每一个操作的均摊成本为3，换句话说，每一个push_back操作的平均成本为$O(1)$。

均摊分析（Amortized Analysis）几种常用的技术:

• 聚合分析，决定n个操作序列的耗费上界$T(n)$，然后计算平均耗费为 $T(n)/n$。
• 记账法，确定每个操作的耗费，结合它的直接执行时间及它在对运行时中未来操作的影响。通常来说，许多短操作增量累加成“债”，而通过减少长操作的次数来“偿还”。
• 势能法，类似记账方法，但通过预先储蓄“势能”而在需要的时候释放。

参考：

• https://zh.wikipedia.org/wiki/%E5%B9%B3%E6%91%8A%E5%88%86%E6%9E%90
• https://johnysswlab.com/the-price-of-dynamic-memory-allocation/