K-Means算法简介
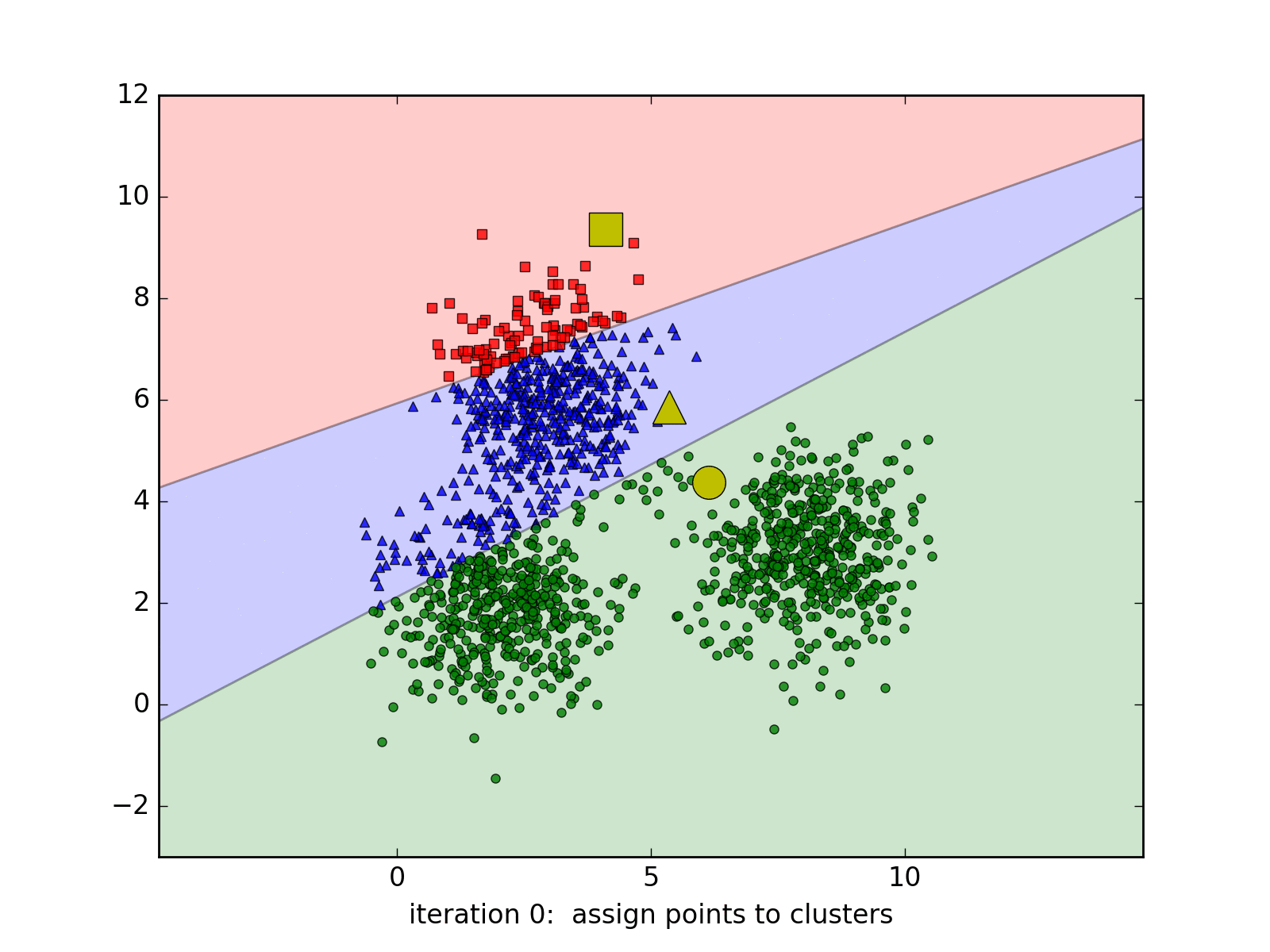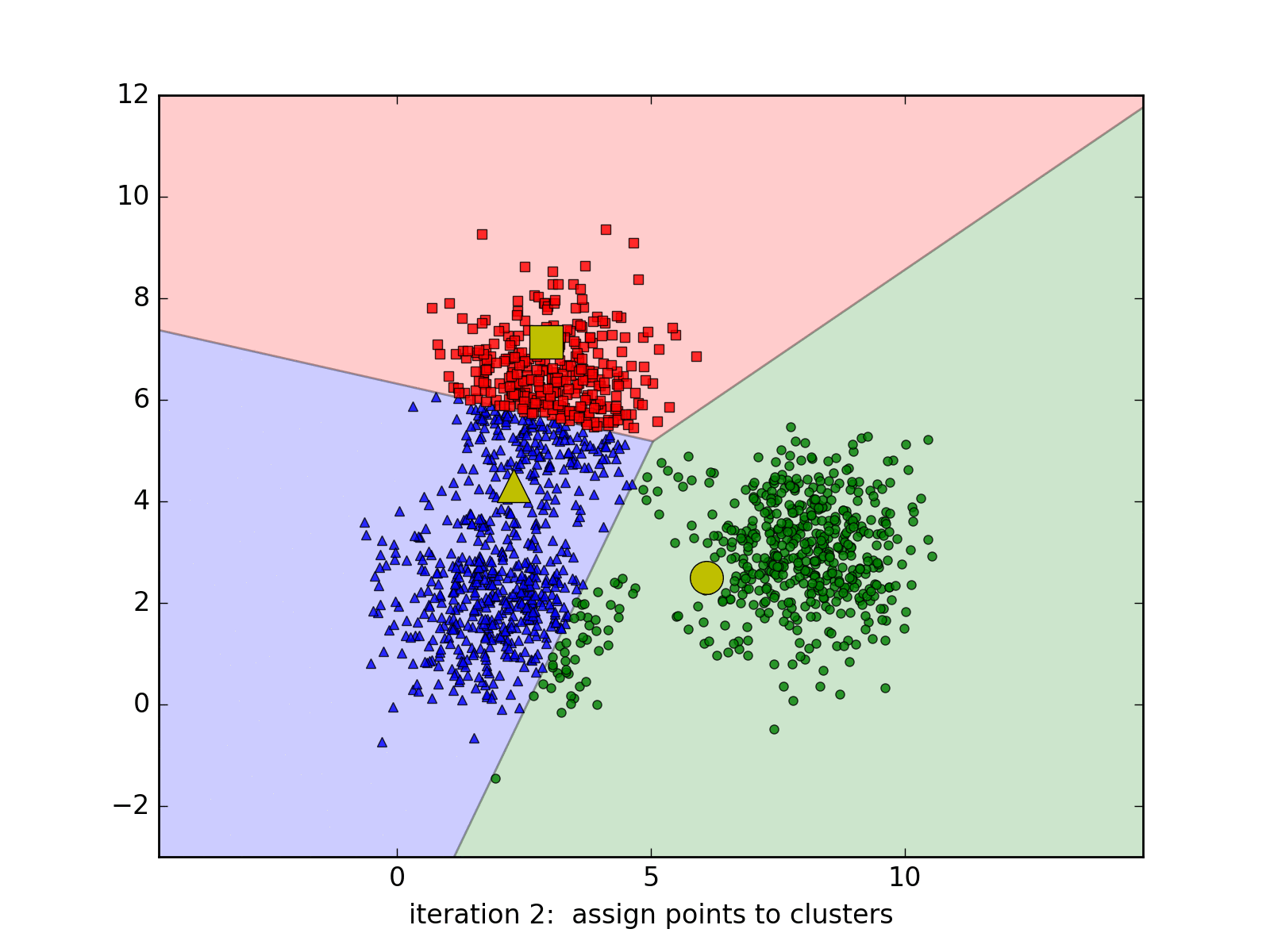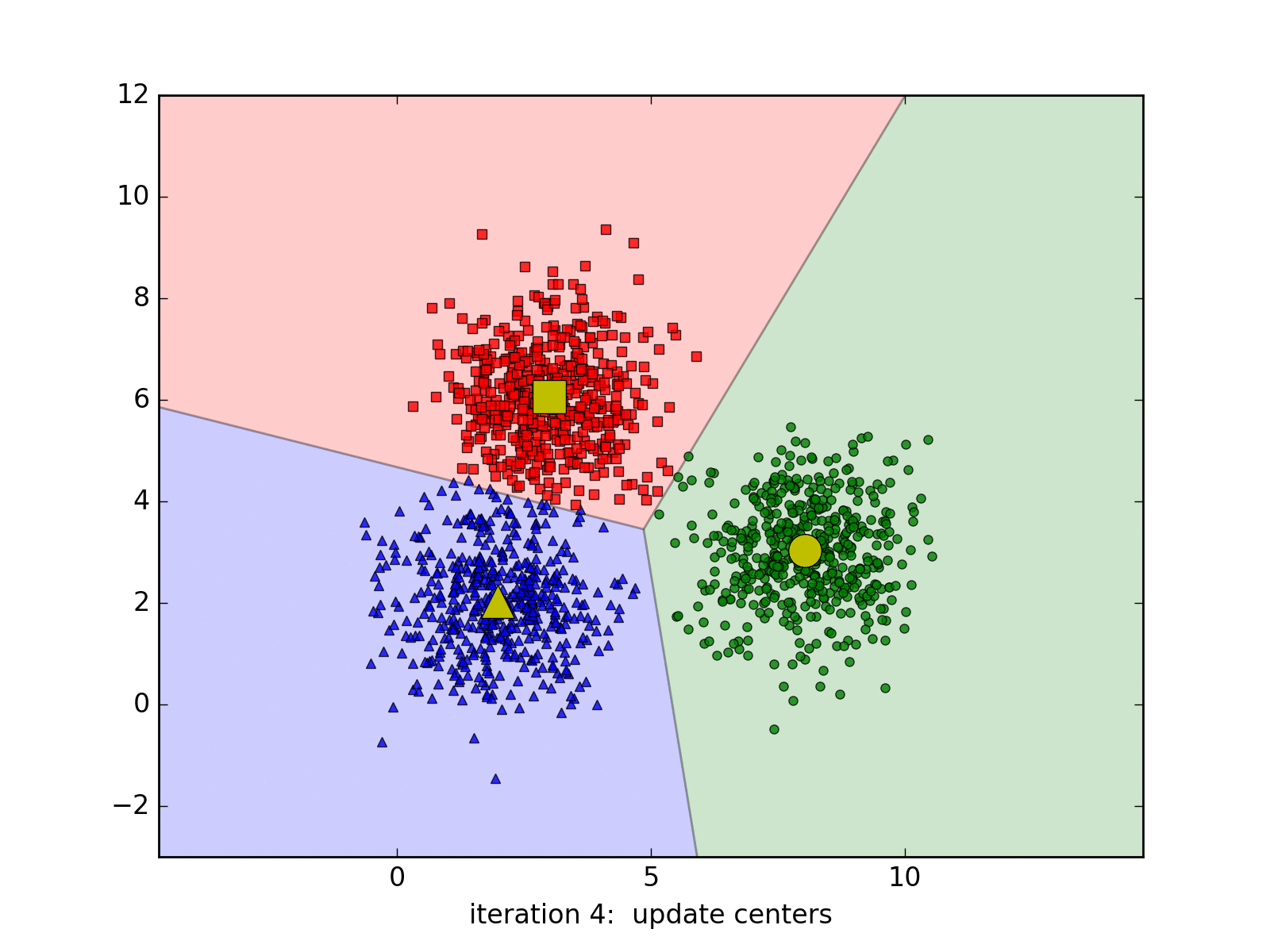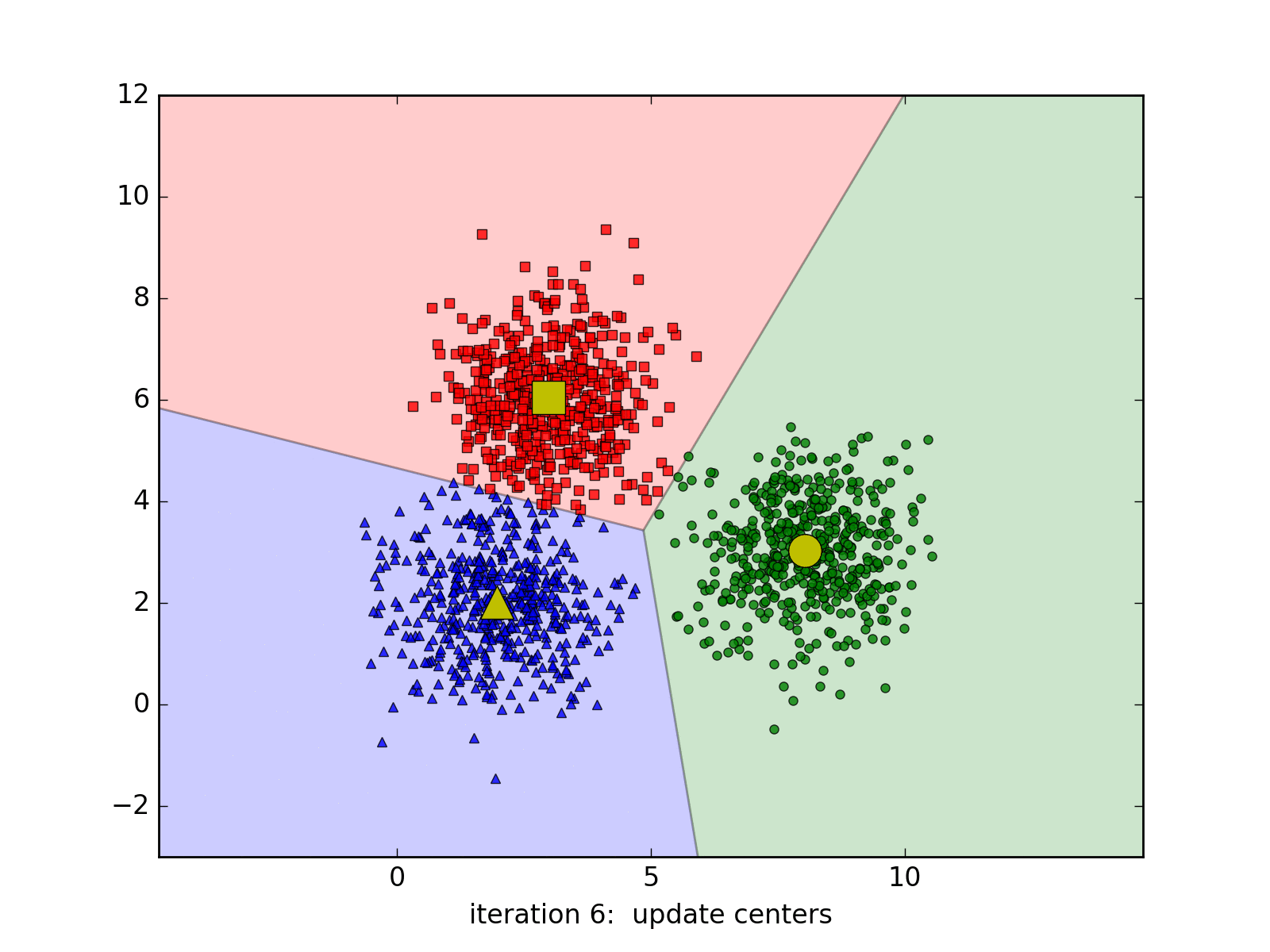
K-Means聚类的目的是:把n个点(可以是样本的一次观察或一个实例)划分到k个聚类中,使得每个点都属于离他最近的均值(此即聚类中心,centroids)对应的聚类,以之作为聚类的标准。这个问题将归结为一个把数据空间划分为Voronoi cells的问题。K-均值是一种通过反复迭代直至收敛到确定值的迭迭代贪婪算法.
K-Means计算是NP-困难的,不过可借助启发式策略快速收敛出一个局部最优解。
算法过程
已知观察集$(x_1,x_2,…,x_n)$,每个观察集都是d维矢量,k-平均聚类要把这n个观测划分到k个集合中(k≤n),使得组内平方和(WCSS within-cluster sum of squares)最小,即它的目标是找到使得下式满足的聚类Si:
其中Ci为类Si类中所有点的均值,即当前类的聚类中心。$arg_{min}$,表示使目标函数f(Si)取最小值时的变量值。
- 首先为聚类任意选出k个初始化的的
聚类中心,每个观察对象被分类到与聚类中心最近的聚类中 - 接着使用当前聚类中的观察对象的
均值,重新计算聚类中心. - 用新计算出的
聚类中心重新对观察对象重复第1步,将每个观察对象被分类到与新的聚类中心最近的聚类中 - 重复1、2步骤直至聚类
聚类中心不再变化,或者小于给定的阈值.
用下面的gif图更好理解:
K-Means算法进行Iris数据聚类
Iris(鸢尾花)数据集以鸢尾花的特征作为数据来源,数据集包含150个数据集,分为3类,每类50个数据,每个数据包含4个属性,是在数据挖掘、数据分类中非常常用的测试集、训练集。现选取3个分类数据中的前25个数据为训练集,后25个数据作为测试集,进行k均值聚类计算,完整代码如下,其中kmeans_train函数即k均值算法的主体部分(迭代,寻找聚类中心直到不再变化的过程)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
#!/usr/bin/python
# -*- coding: utf-8 *-*
'''
Attribute Information:
0. sepal length in cm
1. sepal width in cm
2. petal length in cm
3. petal width in cm
4. class:
-- 0: Iris Setosa
-- 1: Iris Versicolour
-- 2: Iris Virginica
'''
import os
import math
import time
import numpy as np
import matplotlib.pyplot as plot
from mpl_toolkits.mplot3d import Axes3D
from scipy import spatial
# 全局变量
g_train_set = None
g_test_set = None
g_centroids = None
class Config:
DATA_FILE="./iris.data"
CLASSES = {
"Iris-setosa":0,
"Iris-versicolor":1,
"Iris-virginica":2
}
LABEL_NAMES = ["SepalLen","SepalWidth","PetalLen","PetalWidth","Classes"]
def data_import(file,delimiter):
return np.genfromtxt(file,delimiter=delimiter)
# euclidean distance of two 1-D vectors
def vec_distance(a,b):
return spatial.distance.euclidean(a, b)
def test_vec_distance():
a=np.array([[1,2,3,4]])
b=np.array([[1,3,5,4]])
# = sqrt(0+1+4+0)=sqrt(6)=2.2360679775
print(vec_distance(a,b))
def kmeans_test():
global g_test_set
global g_centroids
distances = np.zeros((3,75))
success,mistake=np.zeros(3),np.zeros(3)
target_classes, cur_classes = g_test_set[:,4], np.zeros(75)
for idx,x in enumerate(g_test_set[:,0:4]):
for cls,c in enumerate(g_centroids):
distances[cls][idx]=vec_distance(x,c)
# 每个点属于最近的聚类中心
min_distance = min(distances[:,idx])
for cls,c in enumerate(g_centroids):
cur_classes[idx] = cls if min_distance == distances[cls][idx] else cur_classes[idx]
for idx,x in enumerate(cur_classes):
cls = int(target_classes[idx])
if cur_classes[idx] == target_classes[idx]:
success[cls] = success[cls] + 1
else:
mistake[cls] = mistake[cls] + 1
print success,mistake
pass
def kmeans_train():
global g_train_set
global g_centroids
# 欧式距离向量,大小3x25
distances = np.zeros((3,75))
# 初始聚类中心
#g_centroids = np.array([g_train_set[1:2,0:4],g_train_set[50:51,0:4],g_train_set[59:60,0:4]])
g_centroids = np.array([g_train_set[0:1,0:4],g_train_set[25:26,0:4],g_train_set[50:51,0:4]])
old_centroids = g_centroids
# 目标分类向量,当前分类向量
target_classes, cur_classes = g_train_set[:,4], np.zeros(75)
print "first g_centroids", g_centroids[0],g_centroids[1],g_centroids[2]
# 迭代,直到聚类中心点不再变化
while True:
# 聚类中所有点的步长和的向量
step_sum = np.zeros((3,4))
# 当前聚类中所有点的计数
step_count = np.zeros(3)
# 计算距离向量,聚类中心到每个点的距离
for idx,x in enumerate(g_train_set[:,0:4]):
for cls,c in enumerate(g_centroids):
distances[cls][idx]=vec_distance(x,c)
# 每个点属于最近的聚类中心
min_distance = min(distances[:,idx])
for cls,c in enumerate(g_centroids):
cur_classes[idx] = cls if min_distance == distances[cls][idx] else cur_classes[idx]
# 重新聚类, 寻找新的聚类中心点:当前聚类中所有点的均值, x可能的取值是(0,1,2)代表所在行的聚类
for idx,cls in enumerate(cur_classes):
x = int(cls)
#print idx, x, g_train_set[idx,0:4], step_sum[x]
step_sum[x] = step_sum[x] + g_train_set[idx,0:4]
step_count[x] = step_count[x] + 1
for cls,c in enumerate(g_centroids):
g_centroids[cls] = step_sum[cls]/step_count[cls]
print g_centroids[0],g_centroids[1],g_centroids[2]
if np.array_equal(old_centroids,g_centroids):
# 聚类中心不再变化,收敛完成
kmeans_plot3d()
break
else:
old_centroids = g_centroids
pass
def kmeans_init():
global g_train_set
global g_test_set
datafile = Config.DATA_FILE
data = data_import(datafile,',')
# 读取并合并训练集数组
g_train_set = np.hstack((data[0:25,0:4],np.full((25,1),0)))
g_train_set = np.vstack((g_train_set,np.hstack((data[50:75 ,0:4],np.full((25,1),1)))))
g_train_set = np.vstack((g_train_set,np.hstack((data[100:125,0:4],np.full((25,1),2)))))
# 读取并合并测试集数组
g_test_set = np.hstack((data[25:50,0:4],np.full((25,1),0)))
g_test_set = np.vstack((g_test_set,np.hstack((data[75:100 ,0:4],np.full((25,1),1)))))
g_test_set = np.vstack((g_test_set,np.hstack((data[125:150,0:4],np.full((25,1),2)))))
def kmeans_plot():
global g_train_set
global g_test_set
global g_centroids
# 以0,1,3特征绘制3D图
my_set = g_train_set;
plot.scatter(my_set[0 :25,0],my_set[0: 25,1],marker="x",color="k")
plot.scatter(my_set[25:50,0],my_set[25:50,1],marker="x",color="m")
plot.scatter(my_set[50:75,0],my_set[50:75,1],marker="x",color="c")
plot.scatter(my_set[0 :25,2],my_set[0: 25,3],marker="o",color="k")
plot.scatter(my_set[25:50,2],my_set[25:50,3],marker="o",color="m")
plot.scatter(my_set[50:75,2],my_set[50:75,3],marker="o",color="c")
my_set = g_test_set;
plot.scatter(my_set[0 :25,0],my_set[0: 25,1],marker="x",color="k")
plot.scatter(my_set[25:50,0],my_set[25:50,1],marker="x",color="m")
plot.scatter(my_set[50:75,0],my_set[50:75,1],marker="x",color="c")
plot.scatter(my_set[0 :25,2],my_set[0: 25,3],marker="o",color="k")
plot.scatter(my_set[25:50,2],my_set[25:50,3],marker="o",color="m")
plot.scatter(my_set[50:75,2],my_set[50:75,3],marker="o",color="c")
plot.xlabel(Config.LABEL_NAMES[0]+"/"+Config.LABEL_NAMES[2])
plot.ylabel(Config.LABEL_NAMES[1]+"/"+Config.LABEL_NAMES[3])
plot.autoscale(tight=True)
plot.grid()
plot.show()
def kmeans_plot3d():
global g_train_set
global g_test_set
global g_centroids
# 以0,1,3特征绘制3D图
my_set = g_train_set;
fig = plot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(my_set[0 :25,0],my_set[0: 25,2],my_set[0 :25,3],marker="o",c="r",edgecolor="r")
ax.scatter(my_set[25:50,0],my_set[25:50,2],my_set[25:50,3],marker="o",c="c",edgecolor="c")
ax.scatter(my_set[50:75,0],my_set[50:75,2],my_set[50:75,3],marker="o",c="b",edgecolor="b")
# 聚类中心
ax.set_xlabel(Config.LABEL_NAMES[0])
ax.set_ylabel(Config.LABEL_NAMES[1])
ax.set_zlabel(Config.LABEL_NAMES[3])
ax.plot(g_centroids[0][:,0],g_centroids[0][:,2],g_centroids[0][:,3],marker="^",c="c")
ax.plot(g_centroids[1][:,0],g_centroids[1][:,2],g_centroids[1][:,3],marker="^",c="b")
ax.plot(g_centroids[2][:,0],g_centroids[2][:,2],g_centroids[2][:,3],marker="^",c="r")
plot.autoscale(tight=True)
plot.grid()
plot.show()
if __name__ == "__main__":
# test_vec_distance()
# exit()
# 数据导入
kmeans_init()
kmeans_plot()
# 训练数据,k-means迭代
kmeans_train()
# 检验测试集
kmeans_test()
将所有数据分2组在2D上plot出来如下:
根据训练的结果,以其中三个属性为坐标的训练数据和聚类中心的3D图如下所示
最后对检验集进行分类的结果是[ 25. 24. 18.] [ 0. 1. 7.],即在三个类别中,分类正确的次数(准确率)分别为25(100%),24(96%),18(72%)
欧式距离(Euclidean distance)
在数学中,欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”(即直线)距离。使用这个距离,欧氏空间成为度量空间。相关联的范数称为欧几里得范数。较早的文献称之为毕达哥拉斯度量。在欧几里得空间中,点x =(x1,…,xn)和 y =(y1,…,yn)之间的欧氏距离为:
\[dis(x,y)=\sqrt{\sum_{i=1}^n {(x_i-y_i)^2}}\]参考
iris数据集:http://archive.ics.uci.edu/ml/datasets/Iris
k均值聚类讲解:http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/kmeans.html
k均值聚类讲解:http://people.revoledu.com/kardi/tutorial/kMean/NumericalExample.htm
k均值聚类讲解:http://blog.jobbole.com/16048/