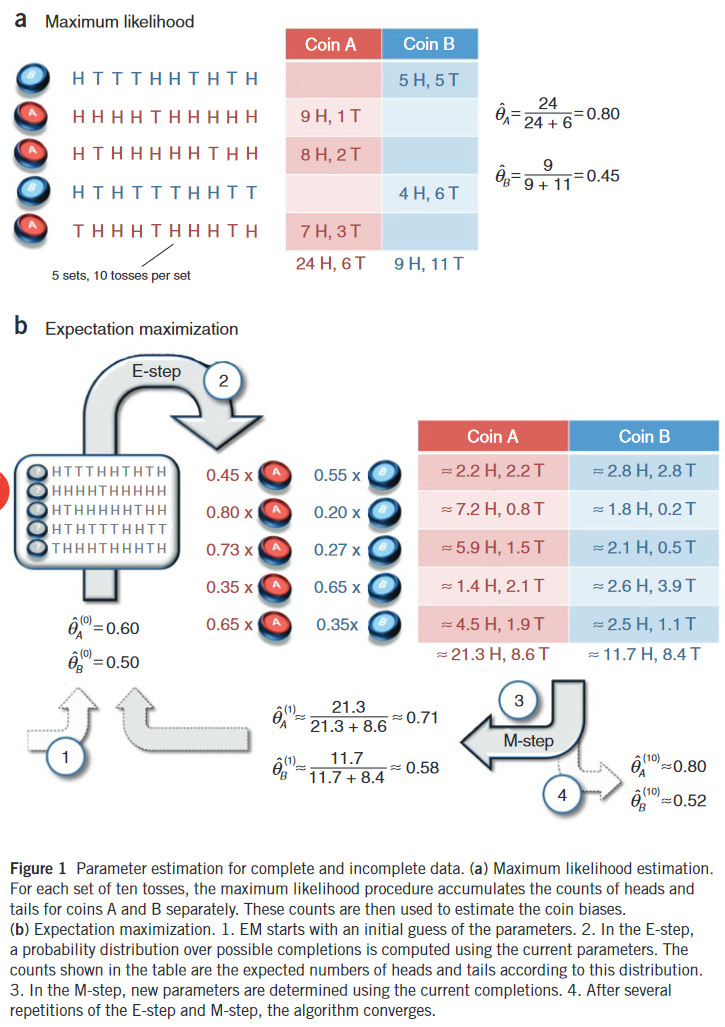
EM算法步骤
(1) 随机初始化模型参数θ的初值 \(\theta_{0}\)
(2) \(j=1,2,...,J\) 开始EM算法迭代:
E步:计算联合分布的条件概率期望:
\[Q_{i}(z_{i})=p(z_{i}|x_{i},\theta_{j})\] \[l(\theta,\theta_{j})=\sum_{i1}^{n}{\sum_{z_{i}}^{}{Q_{i}(z_{i})log\frac{p(x_{i},z_{i};\theta)}{Q_{i}(z_{i})}}}\]M步:极大化 \(l(\theta,\theta_{j})\) 得到
\[\theta_{j+1}=argmaxl(\theta,\theta_{j})\]如果\(\theta_{j+1}\) 已经收敛,则算法结束。否则继续进行E步和M步进行迭代。
输出:模型参数 \(θ\)。
举例
假设现在有两枚硬币1和2,,随机抛掷后正面朝上概率分别为P1,P2。为了估计这两个概率,做实验,每次取一枚硬币,连掷5下,记录下结果,如下:
| 硬币 | 结果 | 统计 |
|---|---|---|
| 1 | 正正反正反 | 3正-2反 |
| 2 | 反反正正反 | 2正-3反 |
| 1 | 正反反反反 | 1正-4反 |
| 2 | 正反反正正 | 3正-2反 |
| 1 | 反正正反反 | 2正-3反 |
可以很容易地估计出P1和P2,如下: \(P1 = (3+1+2)/ 15 = 0.4\) \(P2= (2+3)/10 = 0.5\)
现在我们抹去每轮投掷时使用的硬币标记如下,但目标没变还是估计P1和P2,要怎么做呢?
| 硬币 | 结果 | 统计 |
|---|---|---|
| ? | 正正反正反 | 3正-2反 |
| ? | 反反正正反 | 2正-3反 |
| ? | 正反反反反 | 1正-4反 |
| ? | 正反反正正 | 3正-2反 |
| ? | 反正正反反 | 2正-3反 |
此时我们多了一个隐变量z,可以把它认为是一个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使用的硬币,比如z1,就代表第一轮投掷时使用的硬币是1还是2。但是,这个变量z不知道,就无法去估计P1和P2,所以,我们必须先估计出z,然后才能进一步估计P1和P2。
用EM的方法去估计就是先随便给P1和P2赋一个值,比如: \(P1 = 0.2\)
\[P2 = 0.7\]如果是硬币1,第一轮中得出3正2反的概率为: \(0.2*0.2*0.2*0.8*0.8 = 0.00512\)
如果是硬币2,得出3正2反的概率为 \(0.7*0.7*0.7*0.3*0.3=0.03087\)
然后依次求出其他4轮中的相应概率。做成表格如下:
| 轮数 | 若是硬币1 | 若是硬币2 |
|---|---|---|
| 1 | 0.00512 | 0.03087 |
| 2 | 0.02048 | 0.01323 |
| 3 | 0.08192 | 0.00567 |
| 4 | 0.00512 | 0.03087 |
| 5 | 0.02048 | 0.01323 |
按照最大似然法则可得出第一轮EM中的z_1参数:
第1轮中最有可能的是硬币2
第2轮中最有可能的是硬币1
第3轮中最有可能的是硬币1
第4轮中最有可能的是硬币2
第5轮中最有可能的是硬币1
用z_1参数按照最大似然概率法则来估计新的P1和P2。 \(P1 = (2+1+2)/15 = 0.33\)
可以看一下效果:
| 初始化的P1 | 估计出的P1 | 真实的P1 | 初始化的P2 | 估计出的P2 | 真实的P2 |
|---|---|---|---|---|---|
| 0.2 | 0.33 | 0.4 | 0.7 | 0.6 | 0.5 |
进行多次E、M步骤迭代后,P1、P2将接近真实值。
Reference
- http://ai.stanford.edu/~chuongdo/papers/em_tutorial.pdf
- https://www.jianshu.com/p/1121509ac1dc