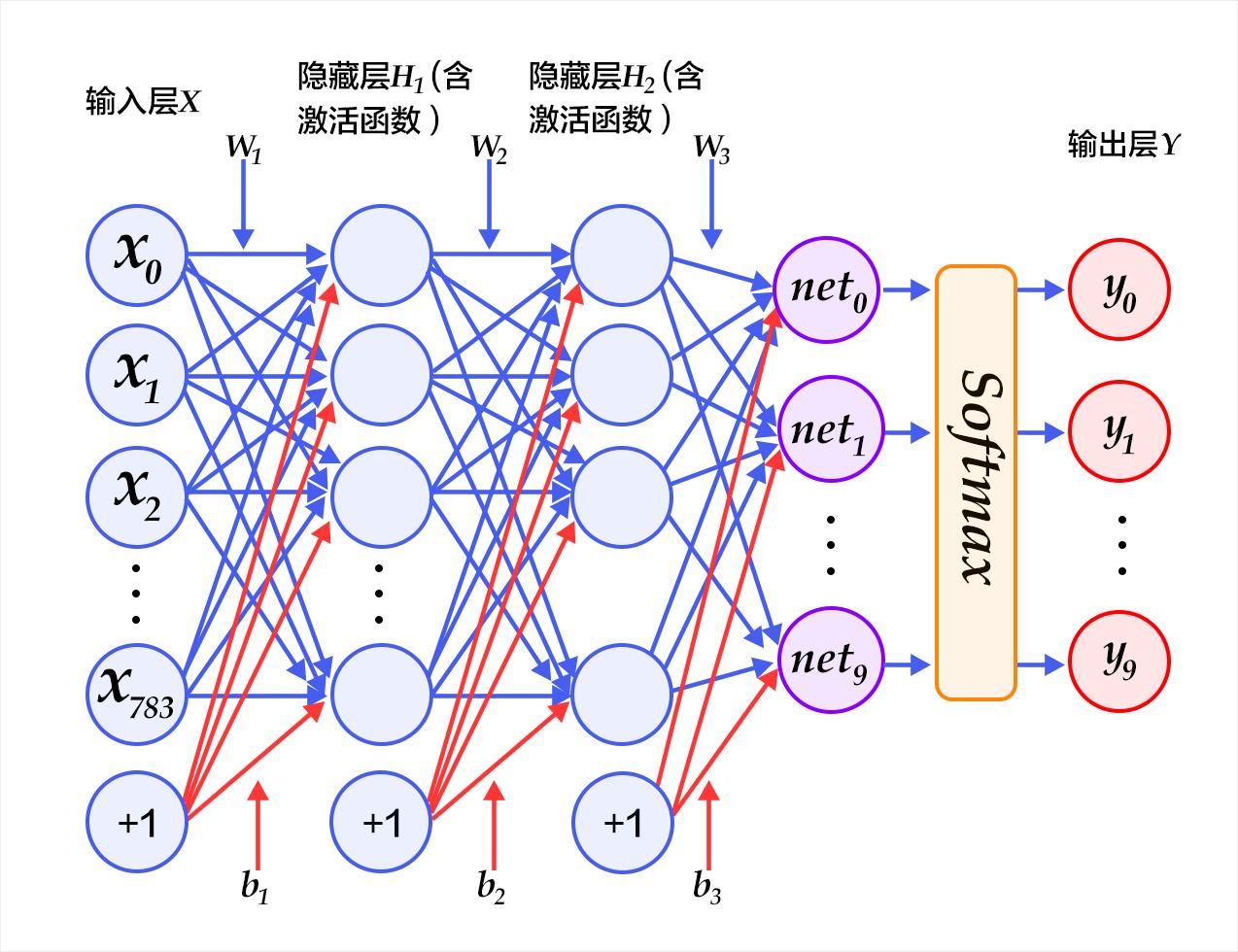
多层感知器
单个感知器只能一刀两半,多个感知器则可以多次分割,直到分割给出想要的分类方式。
网络拓扑
反向传导算法(BP算法)
BP算法是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法计算对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
BP算法过程
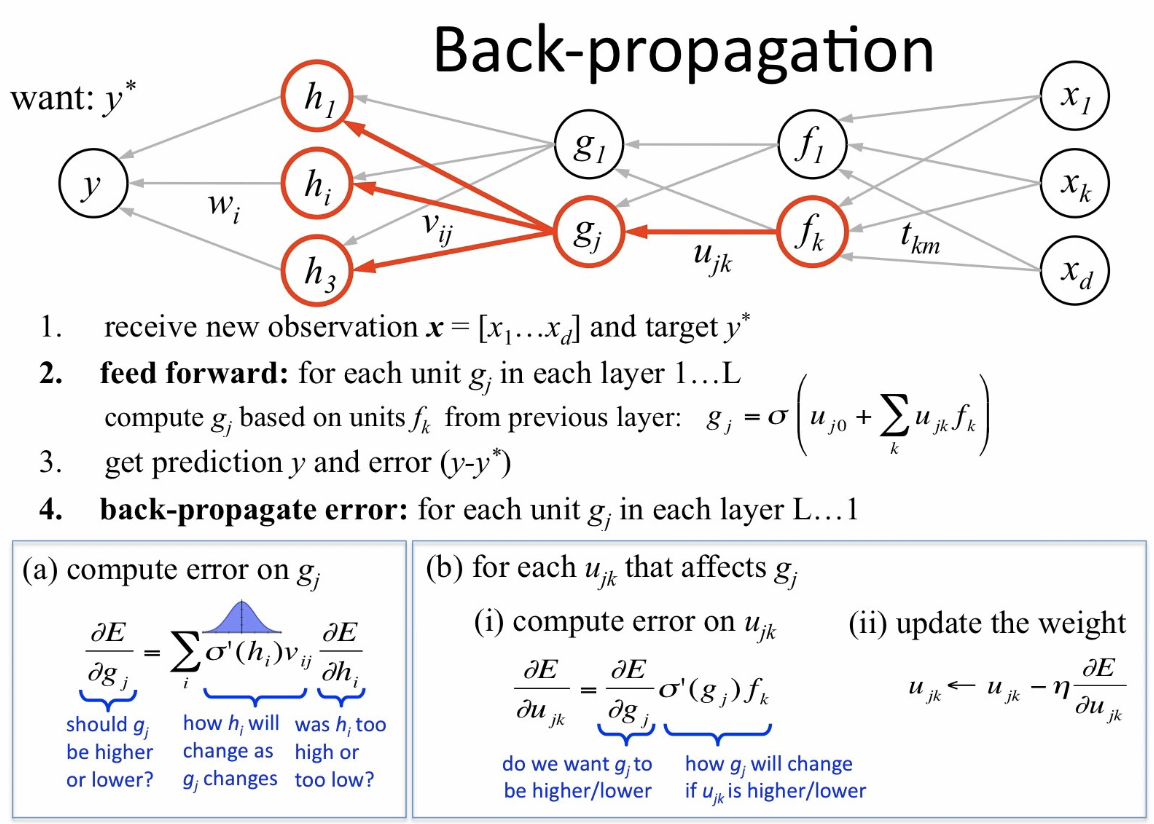
用一张图表示前向(FP)和后向(BP算法,Backpropagation)传播的过程:
BP算法主要由两个阶段:激励传播、和权重更新。
第1阶段:激励传播
每次迭代中的传播环节包含两步:
- 前向传播阶段: 将训练输入送入网络以获得激励响应;
- 反向传播阶段: 将激励响应同训练输入对应的目标输出求差,从而获得隐层和输出层的响应误差。
第2阶段:权重更新
对于每个突触上的权重,按照以下步骤进行更新:
- 将输入激励和响应误差相乘,从而获得权重的梯度;
- 将这个梯度乘上一个比例(学习速度)并取反后加到权重上。
- 这个比例(百分比)将会影响到训练过程的速度和效果,因此称为“训练因子”。梯度的方向指明了误差扩大的方向,因此在更新权重的时候需要对其取反,从而减小权重引起的误差。
第1和第2阶段可以反复循环迭代,直到网络的对输入的响应达到满意的预定的目标范围为止。
算法过程数学描述如下:
- 进行前馈传导计算,利用前向传导公式,得到
L1,L2,...直到输出层L(n-1)的激活值。对输出层
\[\delta^{(n_l)} = - (y - a^{(n_l)}) \bullet f'(z^{(n_l)})\]L(nl),计算残差,进行偏导求算:对于
\[\delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f'(z^{(l)})\]l=nl-1, nl-2, nl-3,... 2的各层,计算:- 计算最终需要的偏导数值:
\(\nabla_{W^{(l)}} J(W,b;x,y) = \delta^{(l+1)} (a^{(l)})^T\) \(\nabla_{b^{(l)}} J(W,b;x,y) = \delta^{(l+1)}\)
其中,$ {\bullet} $ 表示向量乘积运算符
类比理解BP算法
梯度下降法背后的直观感受可以用假设情境进行说明。一个被卡在山上的人正在试图下山(即试图找到极小值)。大雾使得能见度非常低。因此,下山的道路是看不见的,所以他必须利用局部信息来找到极小值。他可以使用梯度下降法,该方法涉及到察看在他当前位置山的陡峭程度,然后沿着负陡度(即下坡)最大的方向前进。如果他要找到山顶(即极大值)的话,他需要沿着正陡度(即上坡)最大的方向前进。使用此方法,他会最终找到下山的路。不过,要假设山的陡度不能通过简单地观察得到,而需要复杂的工具测量,而这个工具此人恰好有。需要相当长的一段时间用仪器测量山的陡峭度,因此如果他想在日落之前下山,就需要最小化仪器的使用率。问题就在于怎样选取他测量山的陡峭度的频率才不致偏离路线。
在这个类比中,此人代表反相传播算法,而下山路径表示能使误差最小化的权重集合。山的陡度表示误差曲面在该点的斜率。他要前行的方向对应于误差曲面在该点的梯度。用来测量陡峭度的工具是微分(误差曲面的斜率可以通过对平方误差函数在该点求导数计算出来)。他在两次测量之间前行的距离(与测量频率成正比)是算法的学习速率。参见限制一节中对此类型“爬山”算法的限制的讨论。
BP算法的激活函数
BP网络都是多层感知机(通常都会有一个输入层、一个隐藏层及一个输出层)。为了使隐藏层能够适合所有有用的函数,多层网络必须具有用于多个层的非线性激活函数:仅用线性激活函数的多层网络会与相当于单层线性网络。常用的非线性激活函数有逻辑函数、柔性最大函数(英语:softmax activation function)和高斯函数。
BP算法证明
参考
中英文对照
- 反向传播算法 Backpropagation Algorithm
- (批量)梯度下降法 (batch) gradient descent
- (整体)代价函数 (overall) cost function
- 方差 squared-error
- 均方差 average sum-of-squares error
- 规则化项 regularization term
- 权重衰减 weight decay
- 偏置项 bias terms
- 贝叶斯规则化方法 Bayesian regularization method
- 高斯先验概率 Gaussian prior
- 极大后验估计 MAP
- 极大似然估计 maximum likelihood estimation
- 激活函数 activation function
- 双曲正切函数 tanh function
- 非凸函数 non-convex function
- 隐藏层单元 hidden (layer) units
- 对称失效 symmetry breaking
- 学习速率 learning rate
- 前向传导 forward pass
- 假设值 hypothesis
- 残差 error term
- 加权平均值 weighted average
- 前馈传导 feedforward pass
- 阿达马乘积 Hadamard product
- 前向传播 forward propagation
参考文档
- http://python.jobbole.com/81278/
- https://zh.wikipedia.org/zh-hans/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
- http://deeplearning.stanford.edu/wiki/index.php/Neural_Networks
- http://ufldl.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95
http://galaxy.agh.edu.pl/%7Evlsi/AI/backp_t_en/backprop.html
- 《神经网络与机器学习》(加拿大)Simon Haykin