[机器学习]人工神经网络初探 - 感知器

人工神经网络(Artificial Neural Net，缩写ANN)，现代神经网络是一种非线性统计性数据建模工具，常用来对输入和输出间复杂的关系进行建模，或用来探索数据的模式。不要被唬住了，ANN做的事其实只有一刀切（单层神经网络），一刀切不清楚的就多切几刀（多层神经网络）。

计算模型

• 人工神经网络由大量的节点（或称“神经元”，或“单元”）和之间相互联接构成。每个节点代表一种特定的输出函数，称为激活函数（activation function）。
• 每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），这相当于人工神经网络的记忆。
• 网络的输出则依网络的连接方式，权重值和激活函数的不同而不同。
• 网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

人工神经网络通常是通过一个基于数学统计学类型的学习方法（Learning Method）得以优化，所以人工神经网络也是数学统计学方法的一种实际应用，通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间，另一方面在人工智能学的人工感知领域，我们通过数学统计学的应用可以来做人工感知方面的决定问题(也就是说通过统计学的方法，人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力)，这种方法比起正式的逻辑学推理演算更具有优势。

适用的问题

反向传播是ANN最常用的算法。他适合以下特征的问题：

• 实例以“属性-值”对表示
• 训练数据可能包含错误
• 可以容忍较长的训练时间
• 可能需要快速求出目标值
• 人类能否理解学到的目标函数是不重要的

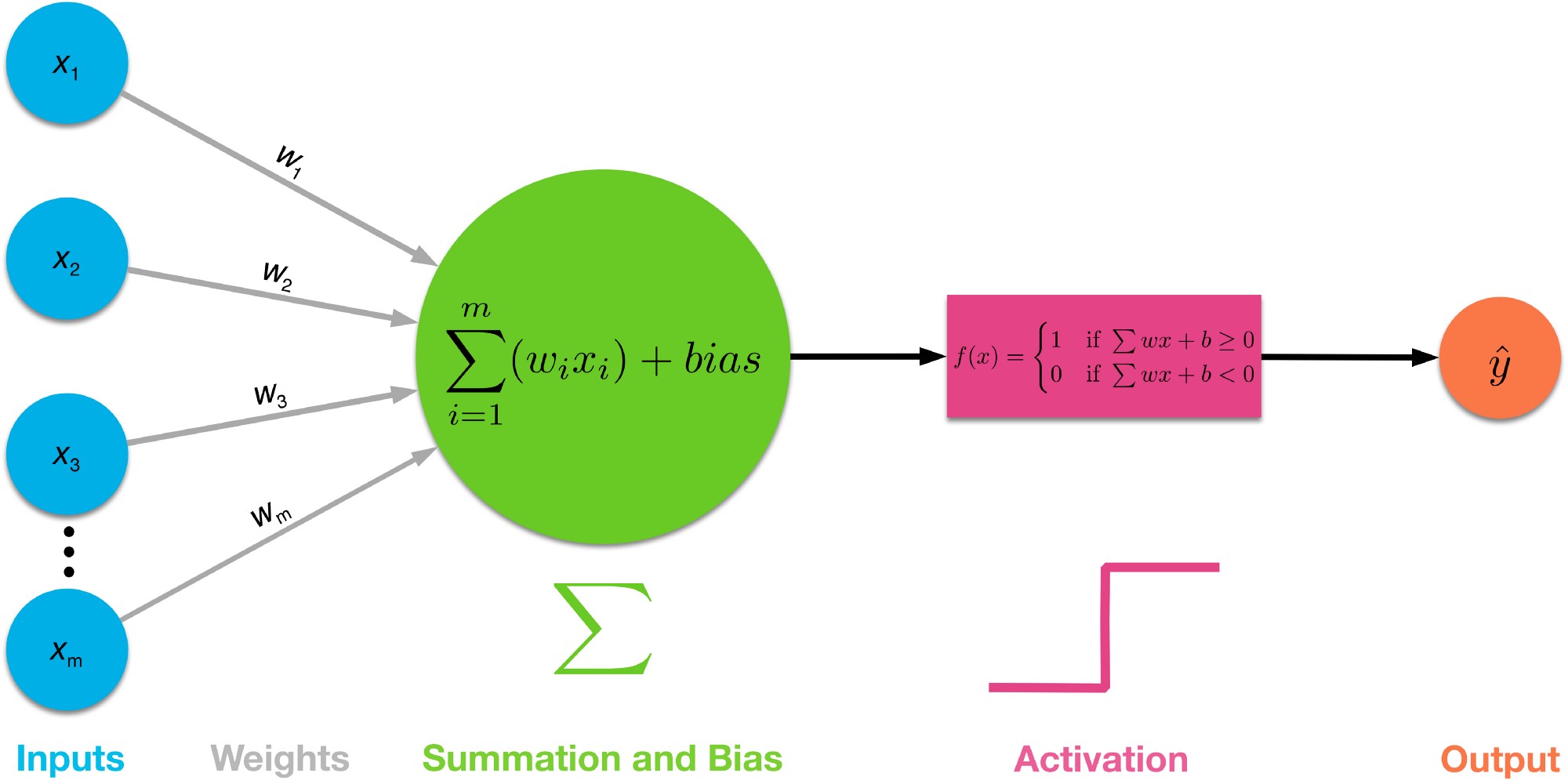
感知器(神经元)

将感知器算法置于机器学习的更广泛背景中：感知器属于监督学习算法类别，更具体地说是单层二值分类器。

神经元（perceptron）示意图：

• $x_1..x_n$为输入向量的各个分量
• $w_1..w_n$为神经元各个突触的权值
• $bias$为偏置
• $f(x)$为传递函数，通常为非线性函数（加法器）。一般有traingd(),tansig(),hardlim()
• 激活函数，用于限制神经输出振幅，使输出信号压制到一定的区域内。
• $y$为神经元输出,{-1,+1}

数学表示： \(y=f(x)=sign(w*x+b)\)

常用激活函数（跃迁函数）

激活函数是一种将数据归一化为标准型或者对称型的方法。

阈值函数(Heaviside函数)

数学表示： \(sign(x) =\begin{cases}+1,&x >= 0\\-1,&x < 0\end{cases}\)

Logistic函数

数学表示： \(f(x)=\frac{1}{1+ae^{-x}}\) Logistic函数输出范围为(0,1)，单调递增，可微分。其中a可以调节倾斜程度。

工作过程

Rosenblatt最初的感知器规则相当简单,可总结为下面两步：

1. 初始化：将权值初始化为0或小随机数。
2. 训练：对每一个训练样本：
   • 计算输出值
   • 更新权值。

权值的更新一般有两种算法，我们称之为感知器法则和delta法则。

感知器收敛：感知器法则

可以表示为：数学表示： \(w_i=w_i+\Delta{w_i}\)

在每个增量中，权值的更新值可由如下学习规则得到： \(\Delta{w_i}= \eta(t_i-o_i)x_i\) 其中ti为目标分类标签，oi为预测标签（感知器输出），η为学习速率（0.0～1.0之间的常数）。简单来说，如果当前输出大于目标输出，则Δw的值为负数，下次计算的值将更偏向目标；反之Δw为正数，下次的输出同样将偏向目标值；η用于控制逼近的速度。

需要注意的是，只有当两个类线性可分才能保证感知器收敛。如果这两个类线性不可分，为避免死循环，我们可以设置一个训练集的最大训练次数，或者是设置一个可接受误分类个数的阈值。

感知器收敛：delta法则和梯度下降算法

当训练样本非线性可分时，根据delta法则可以收敛到一个目标的最佳近似值，delta的关键思想是使用梯度下降(gradient descent)来搜索可能的权向量的假设空间，以找到最佳你和训练样本的权值向量。这个法则为反向传播算法提供了基础。

梯度下降算法证明

1. 对于delta法则，假设有n个输入向量{d1,d2,d3,..,dn}先定义训练误差：

\(E(w)=\frac{1}{2} \sum_{i=1}^n (t_{di} - o_{di})^2\) 这里的1/2是为了抵消求导出来的系数，该表达式会乘以一个任意的学习速率，因此在这里乘上一个常系数是没有关系的。

1. 定义输出：

\(o_{di}=w_i * x_i\) 其中t,o分别为目标输出和实际输出，训练目标即使E(w)尽可能小，因此可以使用求导方法计算调整的方向，E(w)的导数就是对于w的梯度(gradient)。

1. 类似感知器法则，权值的增量Δw现在可以用梯度来确定，将1、2中代入，得到梯度下降算法公式： \(\Delta w_i=\eta \frac {\partial E(w)}{\partial w_i} = \sum_{i=1}^n(t_{di}-o_{di})(-x_{di})\) 其中x_di表示输入向量di中的输入向量x。这样，最陡峭的下降其偏导数越大，权值逼近速度越大。

梯度下降算法描述

gradient-descent (training_examples, η)， x=>输入向量， η=>学习速率，t=>目标输出， o=>当前输出

1. 初始化wi为某个小的随机值

2. 初始化Δwi = 0

3. 对训练集中的每个输入x：
   3.1 计算o = wi*x
   3.2 计算Δwi = Δwi+η(t-o)*xi

4. 更新权值 wi = wi + Δwi

5. 收敛完成退出，否则跳转到步骤2继续梯度下降

一种几何描述方法

右侧的图片示例了这一过程，这里假设F定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数F为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数F值最小的点。

使用ANN（感知器法则）对鸢尾花数据分类

#!/usr/bin/python
# -*- coding: utf-8 *-*

'''
 Attribute Information:
   0. sepal length in cm
   1. sepal width in cm
   2. petal length in cm
   3. petal width in cm
   4. class:
      -- 0: Iris Setosa
      -- 1: Iris Versicolour
      -- 2: Iris Virginica
'''

import os
import sys
import math
import time
import numpy as np
import matplotlib.pyplot as plot
from mpl_toolkits.mplot3d import Axes3D

from scipy import spatial
from matplotlib.animation import FuncAnimation

# 全局变量
g_train_set = None
g_train_target = None
g_test_set = None
g_chars = [0,2]
g_data_step = [0, 50, 50, 100]
#g_chars = [1,3]
#g_data_step = [50, 100, 100, 150]
g_ppn = None

# 一个数据背景，一个数据分割
plot_fig, plot_ax = plot.subplots()
plot_line, = plot_ax.plot(0, 0, 'r-', linewidth=2)

class Config:
    DATA_FILE = "/devel/git/github/SmallData/LearnMLWithPython/ch02/iris/uic-iris-data/iris.data"
    CLASSES = {
        "Iris-setosa": 0,
        "Iris-versicolor": 1,
        "Iris-virginica": 2
    }
    LABEL_NAMES = ["SepalLen", "SepalWidth", "PetalLen", "PetalWidth", "Classes"]


class Perceptron:
    '''
    基本感知器

    Attributes
    -----------
    '''

    def __init__(self, speed=1, train_limit=30, debug=False):
        self.errors = []
        self.speed = speed
        self.debug = debug
        self.train_limit = train_limit
        self.w0 = []
        self.train_count = 0

    # 迭代训练函数
    # x:输入向量
    # y:目标向量
    def train(self, x, y):
        if self.train_count==0:
            # 每个列数即一个属性，每个属性作为一层，分配一个权值，最后加上一个bias偏置的权值
            # bias可以看作一组（[1,1,..,1],b）的输入，数学上等价
            self.weight = np.zeros(x.shape[1])
            self.bias = 0

        self.train_count += 1
        if self.train_count < self.train_limit:
            errs = 0
            for i, val in enumerate(zip(x, y)):
                xi, ti = val[0], val[1]
                # 计算步进向量
                diff = ti - self.active(xi)
                update = self.speed * diff
                # 更新权重向量和偏置
                self.weight += update * xi
                # bias可以看作一组（[1,1,..,1],b）的输入，数学上等价，所以也需要加上步进
                self.bias += update
                errs += int(update != 0.0)
                #print diff
            self.errors.append(errs)
            self.w0.append(self.weight[0])
            print(self.train_count, self.weight, self.bias, errs)

    # 输入计算函数，返回所有信号输出组成的向量
    def input(self, x):
        # 向量点积计算输入向量xi的输出
        return np.dot(x, self.weight) + self.bias

    # 激活函数，简单的阈值函数即可进行分类
    def active(self, x):
        return np.where(self.input(x) >= 0.0, 1, -1)

    def statics(self):
        # 统计迭代过程错误次数（理想情况下错误为0即达到收敛目的）
        plot.plot(range(1, len(self.errors) + 1), self.errors, marker='o', color="c")
        plot.plot(range(1, len(self.w0) + 1), self.w0, marker="^", color="k")
        plot.xlabel('Iterations')
        plot.ylabel('W0/Missclassifications')
        plot.show()


def data_import(file, delimiter):
    return np.genfromtxt(file, delimiter=delimiter)

def ann_test(x,y,ppn):
    for idx,xi in enumerate(x):
        output = np.dot(xi, ppn.weight) + ppn.bias
        print(idx, xi, y[idx][0], output[0])
    pass

def ann_init():
    global g_train_set
    global g_ppn

    datafile = Config.DATA_FILE
    data = data_import(datafile, ',')

    # 读取并合并训练集数组
    g_train_set = np.hstack((data[g_data_step[0] :g_data_step[1],  0:4], np.full((50, 1), -1.0)))
    g_train_set = np.vstack((g_train_set, np.hstack((data[g_data_step[2]:g_data_step[3], 0:4], np.full((50, 1), 1.0)))))
    # g_train_set = np.hstack((data[50:100,  0:4], np.full((50, 1), -1.0)))
    # g_train_set = np.vstack((g_train_set, np.hstack((data[100:150, 0:4], np.full((50, 1), 1.0)))))

    # 准备数据
    g_ppn = Perceptron(speed=0.1, train_limit=50)

def ann_plot_data():
    global g_train_set
    global plot_fig
    global plot_ax
    global g_chars

    my_set = g_train_set
    plot_ax.scatter(my_set[0  :50 ,g_chars[0]],my_set[0  :50 ,g_chars[1]],marker="^",color="k")
    plot_ax.scatter(my_set[50 :100,g_chars[0]],my_set[50 :100,g_chars[1]],marker="o",color="m")
    plot_ax.set_xlabel(Config.LABEL_NAMES[g_chars[0]])
    plot_ax.set_ylabel(Config.LABEL_NAMES[g_chars[1]])

def plot_update(fit):
    global plot_line
    global g_train_set
    global g_ppn
    global g_chars

    # 训练数据
    g_ppn.train(g_train_set[:, g_chars], g_train_set[:, [4]])

    # 更新分割线
    fit = np.array([-g_ppn.weight[0]/g_ppn.weight[1],(-g_ppn.bias[0])/g_ppn.weight[1]])
    fnd = np.poly1d(fit)
    fx = np.linspace(0,8)
    plot_line.set_xdata(fx)
    plot_line.set_ydata(fnd(fx))

    str = ", y=%0.2f*x0+%0.2f*x1+%0.2f=0, train %d"%(g_ppn.weight[0],g_ppn.weight[1],g_ppn.bias[0],g_ppn.train_count)
    plot_ax.set_xlabel(Config.LABEL_NAMES[g_chars[1]]+str)

if __name__ == "__main__":
    # 导入训练集合
    ann_init()
    ann_plot_data()

    # FuncAnimation 会在每一帧都调用“update” 函数,  在这里设置一个10帧的动画，每帧之间间隔500毫秒
    anim = FuncAnimation(plot_fig, plot_update, frames=np.arange(0, 8), interval=500)
    if len(sys.argv) > 1 and sys.argv[1] == 'save':
        anim.save('line.gif', dpi=80, writer='imagemagick')
    else:
        # 会一直循环播放动画
        plot.show()

运行结果如下：

收敛问题

尽管在较低的学习率情形下，因为一个或多个样本在每一次迭代总是无法被分类造成学习规则不停更新权值，最终，感知器还是无法找到一个好的决策边界。

在这种条件下，感知器算法的另一个缺陷是，一旦所有样本均被正确分类，它就会停止更新权值，这看起来有些矛盾。直觉告诉我们，具有大间隔的决策面（如下图中虚线所示）比感知器的决策面具有更好的分类误差。但是诸如“Support Vector Machines”之类的大间隔分类器不在本次讨论范围。

尽管感知器完美地分辨出两种鸢尾花类，但收敛是感知器的最大问题之一。 Frank Rosenblatt在数学上证明了当两个类可由线性超平面分离时，感知器学习规则收敛，但当类无法由线性分类器完美分离时，问题就出现了。为了说明这个问题，我们将使用鸢尾花数据中另外两个不同的类和特性。选取类为Iris-versicolor，Iris-virginica，特征为：sepal width，petal width。

将原始数据绘制在2D坐标如下：

收敛统计：

对于这种不能一刀切的数据，ANN将反复迭代。

参考

中英文对照

• 反向传播算法 Backpropagation Algorithm
• （批量）梯度下降法 (batch) gradient descent
• （整体）代价函数 (overall) cost function
• 方差 squared-error
• 均方差 average sum-of-squares error
• 规则化项 regularization term
• 权重衰减 weight decay
• 偏置项 bias terms
• 贝叶斯规则化方法 Bayesian regularization method
• 高斯先验概率 Gaussian prior
• 极大后验估计 MAP
• 极大似然估计 maximum likelihood estimation
• 激活函数 activation function
• 双曲正切函数 tanh function
• 非凸函数 non-convex function
• 隐藏层单元 hidden (layer) units
• 对称失效 symmetry breaking
• 学习速率 learning rate
• 前向传导 forward pass
• 假设值 hypothesis
• 残差 error term
• 加权平均值 weighted average
• 前馈传导 feedforward pass
• 阿达马乘积 Hadamard product
• 前向传播 forward propagation

参考文档

• http://python.jobbole.com/81278/
• https://zh.wikipedia.org/zh-hans/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
• http://deeplearning.stanford.edu/wiki/index.php/Neural_Networks
• http://ufldl.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95

• http://galaxy.agh.edu.pl/%7Evlsi/AI/backp_t_en/backprop.html

• 《神经网络与机器学习》（加拿大）Simon Haykin